Matemáticas que se pueden tocar
Desafío Creativo 2025
El desafío creativo de este año es construir elementos matemáticos utilizando objetos cotidianos (artículos domésticos, objetos de la naturaleza o incluso personas). Utilizando arte y creatividad (¡el tema de este año!) pueden crear esculturas que lleven las matemáticas del papel al mundo real.
Construir elementos matemáticos como
- figuras geométricas,
- patrones o secuencias,
- fórmulas,
- números y símbolos matemáticos,
- curvas y espirales,
- cuadrados mágicos y otros acertijos matemáticos,
- teselaciones,
- fractales,
- ¡y más!
… utilizando cosas de todos los días como:
- tenedores, cucharas y otros utensilios de cocina,
- monedas, llaves y botones,
- libros, lápices, clips y bandas elásticas,
- ramitas, hojas y piedritas de la naturaleza,
- calcetines, cordones y otras prendas de vestir,
- tazas, tazones y platos,
- palillos y plastilina,
- pasta seca, frutos secos y dulces,
- tus amigos y tu familia
- ¡y cualquier otra cosa que se les ocurra!
Algunos ejemplos e idéas

Construir cuerpos geométricos y otras estructuras usando palillos y plastilina. [1]

Representar ideas matemáticas utilizando flores, frutas y verduras. [2]

Crear diferentes tipos de estructuras matemáticas utilizando papel, tela y otros materiales. [3]

Hornear galletas que sigan un patrón de teselación, como la “baldosa de Einstein” (la pueden encontrar en la página 10 de este archivo; también hay un cortador imprimible en 3D disponible ). [4]
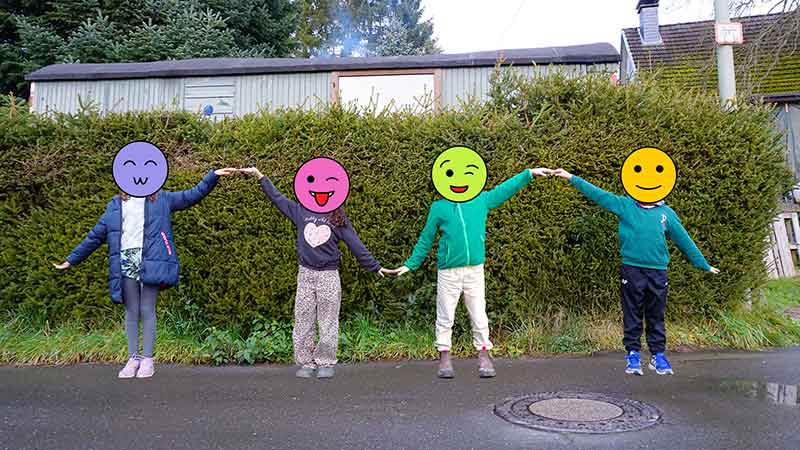
Crear un patrón repetitivo (como esta onda sinusoidal) con la ayuda de tus amigos. [5]
Envíen una foto de su obra
Tienen tiempo de enviarnos una foto hasta el
10 de marzo del 2025
usando el formulario linkeado a continuación. Publicaremos una galería de algunas de las mejores fotos que recibamos.
Sígannos en redes sociales o
suscríbanse a nuestro boletín
para recibir anuncios sobre el desafío.
Todos pueden participar. Compartan el desafío en su escuela, colegio o universidad. ¡Pueden participar en equipo!
El desafío ha terminado. Ver los resultados.
Reglamento del desafío
- El desafío estará abierto hasta el final del 10 de marzo del 2025.
- Envíen una foto de un elemento matemático construído utilizando objetos cotidianos (ejemplos más arriba). Pueden posar, junto con otras personas, junto a su obra. Nos encantaría ver dónde viven, así que aprovechen la oportunidad para mostrarnos su ciudad, pueblo, aldea, el paisaje que los rodea, su escuela o lugar de trabajo.
- Pueden enviar más de una foto, pero cada una debe ser de una creación distinta.
- Asegúrense de obtener el consentimiento de cualquier persona que aparezca en la foto. Si menores de edad aparecen en la foto, deben obtener su consentimiento y también el de sus padres, madres o guardianes legales.
- Si quieren proteger su identidad o la de cualquier otra persona, o prefieren no mostrar su rostro por cualquier razón, siéntanse en libertad de utilizar una máscara, anteojos y una peluca, o cubrirse utilizando un emoji (pueden usar nuestras caritas oficiales del IDM).
Detalles técnicos
- Envíen sus fotos en formato JPEG.
- Las fotos cuadradas (1:1) son las que mejor quedan. Pero también es posible enviar fotos en encuadre vertical (retrato) u horizontal (apaisado).
- En lo posible utilicen una resolución de 1200x1200 píxeles o superior, pero idealmente no por encima de 4800x4800 píxeles.
Consejos para sacar una buena foto de su obra

- Regla de los tercios: Si se divide el área de la fotografía en tercios tanto vertical como horizontalmente, las partes clave de la foto deben estar situadas en la intersección de las divisiones.

- El espacio que rodea al sujeto de una foto se llama “espacio negativo.” Asegúrense de que su imagen incluya suficiente espacio negativo para equilibrar el área del sujeto. La composición mejorará si prestan especial atención al espacio negativo al encuadrar su foto.
- Asegúrense de que la fuente de luz (el sol o la lámpara) esté delante del sujeto, para que lo ilumine de frente.
- Asegúrense de que la cámara no se mueva para evitar fotos borrosas. Se recomienda apretar los brazos contra el cuerpo, exhalar y pulsar ligeramente el obturador. Otra opción es utilizar algún objeto para apoyar la cámara o usar la función de temporizador.
- ¡Muestren su obra en contexto! Su foto va a ser más interesante si muestra el lugar donde fue tomada, o si incluye a las personas que participaron en la creación.
Arte para inspirarse
A lo largo de la historia, muchos movimientos artísticos (como el arte Concreto y Neo-Concreto, el Constructivismo y la Bauhaus) crearon esculturas (así como edificios y otros objetos) utilizando formas y disposiciones geométricas.
El arte cinético utiliza el movimiento de la obra o del espectador para crear efectos interesantes. Con frecuencia, se basa en las matemáticas para sus construcciones.
El “Land art” (o arte ambiental) es un tipo de arte que emplea materiales naturales (como tierra, rocas, vegetación, agua, etc.) para crear obras en el paisaje.
Esta coreografía de Sadeck Berrabah es un hermoso ejemplo de formas geométricas creadas con cuerpos humanos.
El origami modular crea formas matemáticas complejas al combinar muchas copias de módulos pequeños y simples.
“El MegaMenger puede ser el fractal más grande jamás construido, hecho con más de un millón de tarjetas de presentación y abarcando todo el planeta.”
Créditos de las imágenes
- [1] Foto por Savino Longo (Bari, Italia), publicada bajo la licencia Creative Commons CC BY-SA 4.0 [creativecommons.org]. Recortada y recoloreada a partir del original.
- [2] Foto por Nurul Wahyuni (Lubuklinggau, Sumatra Meridional, Indonesia), publicada bajo la licencia Creative Commons CC BY-SA 4.0 [creativecommons.org]. Recortada y recoloreada a partir del original.
- [3] Foto por Beril Naz Ülgen (Erenler (Sakarya), Turquía), publicada bajo la licencia Creative Commons CC BY-SA 4.0 [creativecommons.org]. Recortada y recoloreada a partir del original.
- [4] Foto por Nikolay Tumanov [x.com], utilizada con permiso. Recortada a partir del original.
- [5] Foto por Imaginary gGmbH, publicada bajo la licencia Creative Commons CC BY-SA 4.0 [creativecommons.org].